Period Doubling
by Prof. Ari Lehto
Starting from Planck quantities, the Period Doubling mechanism produces precise predictions to stable structures ranging from elementary particles to celestial systems. The buildup of structures in space is governed by the simplest possible law of nature, Period Doubling, which is a universal property of nonlinear systems. PD discloses the system of elementary particles as well as the law behind planetary orbits.
Ari Lehto, Period-Doubling as a Structure Creating Natural Process
La Nuova Critica, Special Issue 63-64, ISSN 1824-9663 (2016), Scientific Models and a Comprehensive Picture of Reality, pp. 91-115. VIDEO.
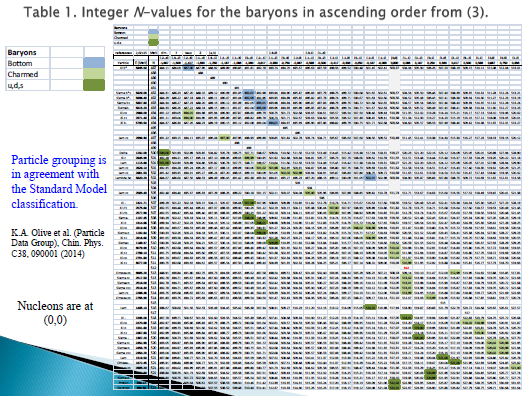
Proton and neutron intrinsic structures
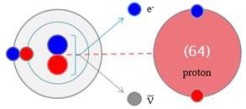
The Planck energy can be calculated either from the conventional Planck mass or defined using the electron-positron pair rest energy. The latter gives extremely simple structures and accurate rest masses for the proton and the neutron indicating that the conventional Planck mass is a little off. PFS Seminar presentation 22.2.2016, Ari Lehto. In the period doubling scenario the neutrino appears quite naturally from the neutron decay, and it seems to be an uncharged partner of an electron (or a positron) originating from the decay of an excited electron-positron pair.
Ari Lehto, On the Planck Scale and Properties of Matter
Special Issue: Quantum Vacuum, Fundamental Arena of the Universe: Models, Applications and Perspectives. Vol. 2, No. 6-1, 2015, pp. 57-65.doi: 10.11648/j.ijass.s.2014020601.17. Full PDF paper
Period doubling, or a frequency halving sequence, is a common property of nonlinear dynamical systems. Period can be related to other physical quantities, e.g. length, energy and temperature, which obtain the corresponding doubling/halving behavior. It is found that physical properties of natural phenomena, systems and elementary particles can be derived directly from the Planck time, taken as the fundamental period. Analysis of experimental data suggests that the period doubling process takes place in three and four internal degrees of freedom. It is further found out that long term stability complies with the stability condition of nonlinear dynamical systems. A theory of period doubling in 1/r-type nonlinear systems with three and four internal degrees of freedom is presented.
Ari Lehto, Elementary particle classification

August 2015 - Ari Lehto, one of the founders of the Physics Foundations Society, has introduced a period-based classification for the elementary particles. Starting from Planck units, the classification appears as a consequence of a period doubling mechanism, which is a universal property of nonlinear dynamical systems. By allowing 3 degrees of freedom for mass energy structures and 4 degrees of freedom for electromagnetic energy structures, the known elementary particles are ordered according to the total number of period doublings forming a system in full agreement with the classification given by the Standard Model of Elementary Particles. The model allows exact calculation of the rest energies of the known particles and there is no need for the quark hypothesis. It also proposes sites for possible particles still missing from the particle listing.
- A preliminary presentation can be opened here.
Selected papers and presentations on period doubling
- Lehto, A. Lepton Pair Production with Only One Charge Available - Neutrino. Preprints 2021, 2021010538. https://doi.org/10.20944/preprints202101.0538.v1
- Lehto, A. Period Doubling Phenomenon as the Origin of Electron Properties. Preprints 2020, 2020060076
- Sipilä, H.; Lehto, A. Fundamental Constants in Time from the Big-Bang. Preprints 2020, 2020070239. https://doi.org/10.20944/preprints202007.0239.v1
- Ari Lehto, Period Doubling Phenomenon as the Origin of Electron Properties Fundamental Journal of Modern Physics ISSN: 2249-9768 Vol. 17, Issue 2, 2022, Pages 131-142 Download Article
Abstract: In the Standard Model of elementary particles, the rest mass, magnetic moment and electric charge of the electron are considered to be natural constants. In this article, it is proposed that these properties can be calculated in a simple way from the corresponding Planck units using the well-known period doubling phenomenon in nonlinear dynamical systems. Periods corresponding to the values of the electron and positron properties belong to a subset of stable periods. The periodic structures of the rest energy and magnetic moment consist of three internal degrees of freedom, whereas the Coulomb energy of the electric charge consists of four. The number of period doublings for the elementary charge determines the value of the fine structure constant alpha.
- Ari Lehto, On the Planck Scale and Structures of Matter, NPA Conference, Storrs, University of Connecticut, May 25-29, 2009 Full text/pdf, Presentation slides ppt/pdf
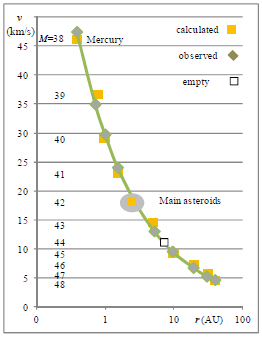
Abstract: Invariant properties and structures of matter are modeled by internal period-like degrees of freedom. Invariance then means periods, which remain unaltered over time. Period doubling is a phenomenon common to nonlinear dynamical systems. In this model the doubling process is generalized into multiple dimensions and utilized to bring about sub-harmonic frequencies, which generate decreasing energies and increasing sizes. It is assumed that period doubling takes place at the Planck scale, and therefore the Planck units are used as reference. The sub-harmonics can be converted into several other physical quantities by well known physical relations. A certain class of sub-harmonics is stable and the elementary electric charge (squared), rest energies and magnetic moments of the electron-positron and proton-antiproton pairs are shown to belong to this class. It is suggested that the structure of the Solar system results from period doubling, too.
- Ari Lehto, On the Planck Scale and Properties of Matter, Nonlin. Dyn. 55, 279-298 (2009)
Abstract: Invariant and long-lived physical properties and structures of matter are modeled by intrinsic rotations in three and four degrees of freedom. The rotations are quantized starting from the Planck scale by using a nonlinear 1/r potential and period doubling - a common property of nonlinear dynamical systems. The absolute values given by the scale-independent model fit closely with observations in a wide range of scales. A comparison is made between the values calculated from the model and the properties of the basic elementary particles, particle processes, planetary systems, and other physical phenomena. The model also shows that the perceived forces can be divided into two categories: (1) force is always attractive, like in gravitation and (2) force is attractive or repulsive, like in electrostatics.
- Ari Lehto, Quantization of Keplerian Systems, http://arxiv.org/abs/physics/0611100 (2006)
- Ari Lehto, Periodic Time and the Stationary Properties of Matter, Chin. J. Phys., Vol. 28, no. 3, June 1990
- Ari Lehto, On (3+3)-Dimensional Discrete Space-Time University of Helsinki, Report Series in Physics, HU-P-236 (1984).
Links
- Prof. William Tifft's book Redshift, key to Cosmology
- William Tifft's blog at the Scientific Association for the Study of Time in Physics and Cosmology (SASTPC)